| May 2009 Index | Home Page |
Editor’s Note: In 1962, I attended a presentation on artificial intelligence by Professor Herbert A. Simon from Carnegie-Mellon University. With Allen Newell, he gained renown in the mid-1950s when they created the first "thinking machine" and launched the field of artificial intelligence using computer models to study human thought processes. Their research was based on a theoretical model called the Turing Machine. Fifty years later, this model continues to be the criterion for studies on human intelligence and learning.
Imagination Effect in Teaching and Learning of Turing Machine
R S Tiwari, S N Deore
India
Abstract
This paper presents the study on application of imagination effect on teaching and learning processes carried out for computing course on “Theoretical Computer Science”. Experiments on high element interactivity topics namely Turing machine, Finite Automata and Push Down Automata were conducted to observe the imagination effect on teaching as well as learning. The current paper reports the work conducted for the Turing Machine. The study used experimental design with two groups, a control and an experimental group, each having 15 students. The control group was taught using traditional methods of lecturing and problem solving followed by physical study and practice with problems. The experimental group was provided a treatment that consisted of lecturing and problem solving followed by mental imagination of procedures required to get solutions for the given problems.
Keywords: Turing Machine, cognitive load, imagination effect, element interactivity, cognitive architecture, intrinsic load, worked example, finite automata, push down automata, working memory, schema.
Background
In 1936 Alan Turing (Hodges, Mrch, 1992) devised a theoretical machine whose computational ability has yet to be surpassed by any concrete and physical computing machine developed by man. Alan Turing’s invention is called Turing Machine and it is a purely hypothetical machine, a computing system that operates using finite series of symbols. It is useful for teaching the philosophical background of basic computing because fundamental ideas regarding computing are still the same as those used in working the Turing Machine. The basic principles underlying the workings of the Turing Machine are equally applicable to modern computers. No machine has been devised so far which can do some advanced computing task that cannot be done by the Turing Machine provided an infinite amount of time and an infinite amount of memory is made available. Hence, it has become mandatory to teach the Turing Machine in particular and formal languages in general. Curricula of computer science of various universities all over the world incorporate a course in Theoretical Computing.
The theory of computing has evolved from linguistics, engineering, logic and mathematics. Turing’s celebrated work on computational functions is the foundation for building a logical framework for computing. The work of Church (Rowland, 2009) and Kleene (Kleene, 1952; Sakharov, 2009) on recursive functions, Post’s (Post, 1943) and Markov’s work string manipulation systems, Shannon’s work on application of Boolean algebra to switching networks, Moore and Mealy’s (Mealy, 1955) work on the finite state machines, Kleene’s work on regular sets, and Chomsky’s work on formal grammars and languages form strong pillars of the logical framework of computing. The major topics covered in the theory of computer science are algorithms, machines, recursive functions, grammars and computation. Traditionally, an academic course on theoretical computer science consisting of topics like Finite Automata, Push-Down Automata, Turing Machines, formal languages, and regular expressions are perceived to be dry and monotonous to teach. The amount learned by students depends upon the instructional design used to develop study material and the methods, tools and techniques used by the teachers in the classroom. The content covering formal languages, theory of Automata and Turing Machine has a high degree of dependency on various concepts, rules, algorithms and procedures used in computer science. The interrelationship of concepts and procedures demand a lot of mental resources for students to understand the subject.
To comprehend the Turing Machine, students need to bring all the related content into their working memory and try to relate this content with their pre-existing knowledge. Moreover, students have to practice problem solving on the Turing Machine. During problem solving, teachers and students draw a series of diagrams on the blackboard and in their respective notebooks. For processing an input string, they have to show head movements and transitions of states of the machine. This is a time consuming and tedious task resulting in low efficiency in solving problems.
The investigators in this study conducted a series of experiments to study “imagination effect” on solving problems related to the Turing Machine. The research findings suggest that if students are encouraged to solve Turing Machine problems through “mental processing of head movements and state transitions”, their performance in achievement tests increases.
Cognitive Load Theory
Cognitive load theory is an instructional theory based on our knowledge of human cognitive architecture (Clark Ruth Colvin, 2006). It has been used to generate a variety of instructional effects (Pass, 2003; Pass F., 2004) that provide demonstrations of effective instructional practice. The Cognitive Load Theory is a major theory of learning and problem solving (Sweller J., 1988; Chandler P., 1991; Sweller John, 1998). It provides a set of guidelines useful for instructional design of study material for teaching and learning purpose. The theory views the human mind as an information processing system. It corresponds to input, processing and output component stages of a computer. The human mind is modeled to have an architecture which consists of three basic components, Sensory Memory, Working Memory and Long-term Memory (Shiffrin & Atkinson, 1969). The information from the outside world is first received through the human senses which are decoded in the sensory memory and subsequently sent to the working memory for further processing. During processing of information in the working memory, the relevant pre-existent information is retrieved from the long term memory and used in deriving the meaning of the given content. The part of the meaningful information processed in the working memory is stored into the long term memory. The human consciousness arises due to the information being processed in the working memory. Unless the mental resources are applied to retrieve information from the long term memory, humans are not always aware of the knowledge that is stored in the long term memory. The storage capacity of long term memory is virtually unlimited. On the contrary, the capacity of storage of the working memory is finite ranging between 5 to 9 units of information which G. A. Miller (Miller, 1956) coined the famous term, "the magical number seven plus or minus two". However, the exact storage capacity of the working memory is shown to depend upon a number of factors like age, health, fatigue, type of item, content familiarity, and education (Baddeley A., 1994; Shiffrin R. M., 1994; Stoltzfus E. R., 1996).
The knowledge in the long term memory is stored in the form of schemas which are hierarchical structures of concepts and their relationships. The mechanisms of Schema Formation (Chi, 1982; Schneider, 1977; Shiffrin R. &., 1977) are useful in overcoming the finite limits of working memory. Meaningful items are grouped and form a chunk which is stored in a separate schema which in turn is treated as a single entity when brought into the working memory. Thus, a large amount of information (facts, concepts, situations etc.) can be processed by the working memory by remaining within the limits of the magic number “seven”.
The processes carried out by humans are also stored in the form of schemas (scripts) in the long term memory. When certain processes are repeatedly performed by humans in their day-to-day lives, humans develop the ability to perform those processes automatically (perform without being aware of them) over a period of time. This is known as schema automation. For example, people talk on cell phones while driving vehicles. We can read paragraphs of text line by line without concentrating on individual letters of the alphabet.
People become expert when they develop schema automation for a number of processes in their field of specialization. At an expert level, people are able to select and use complex schemas and automated processes to reduce the cognitive load that arises during processing of information in the working memory.
Instructional Techniques and Imagination Effect
Scientists have studied various instructional effects which are derived from cognitive load theory. Several instructional techniques have been evolved on the basis of these effects (Cooper G., 1998). Some of the main effects are: worked example and problem completion effect, goal free effect, split attention effect, redundancy effect, modality effect and imagination effect. The instructional material designed on the basis of these effects enables the cognitive load to be kept within the limits of the working memory.
The worked example effect suggests that instructional material should include varied worked-examples. In the problem completion effect, students are presented with partially completed worked examples. This effect has similar benefits on learning. When students are not familiar with a specific problem type, they use a problem solving strategy called means-ends analysis (Larkin, 1980). In this strategy, students solve the given problem by following steps which reduce the difference between the current problem state and the goal state. Often, students have to switch between working from current state to goal state and from goal state to current state. This imposes heavy cognitive load on students. Instead of giving goal-directed problems, goal-free problems reduce the cognitive load. In goal free problems, no specific goal state is given to the students. Instead, students are asked to solve what they can.
Usually, instructional material printed in books as well as material presented on black/white boards contain text and graphics. When graphics and the associated text are located at different positions, students have to frequently shift their attention between graphics and text. This leads to high value of cognitive load which can be reduced by integrating text into the graphics.
The worked examples show students the steps required to solve a given type of problem that promotes acquisition of schemas and automation. Thus, students acquire knowledge and skills required to identify the type of problem and the procedure (steps) required to solve problems of each particular type. The worked examples impose a low level of cognitive load because students have to pay attention to only two problem states at a time and the rule that connects them. Worked examples are presented to the students in alternating sequence consisting of worked example and the problem to be solved so that students can focus their attention on the problem type and the associated procedure.
The worked examples help limit the cognitive load on working memory. Traditionally, students are taught to solve problems using means-ends analysis which works by reducing differences between the stated goal and the given problem. Consequently, means-ends analysis may be rendered inoperable by redefining the problem goal so that no obvious goal exists (for example, "find what you can"). This is the principle behind the generation of goal-free problems. If problems are "goal free" then a problem solver has little option but to focus on the information provided (the given data) and to use it wherever possible. This automatically induces a forward working solution path similar to that generated by expert problem solvers. Such forward working solutions impose very low levels of cognitive load and facilitate learning.
Imagination effect involves mentally simulating the functioning and interaction of elements. Student learning is improved when they are instructed to imagine the processes covered in their study material. This phenomenon is called imagination effect. The imagination effect occurs when learners imagining a procedure or concept perform better on a subsequent test than learners who study material physically. Cognitive load theory predicts that information is more likely to be transferred from working memory to long-term memory under imagination conditions. Cognitive theory has been used to explain the effect by suggesting that when learners imagine information, they process the relevant schemas in working memory, which facilitates automation. It also suggests that effectiveness of the imagination effect depends upon the number of cognitive elements contained in the problem and the prior knowledge of the students. Mental practice is supposed to enable schema automation.
Various terms for “imagining”, e.g. symbolic rehearsal and imaginary practice, are used in the literature. The imagining or mental practice is “…the cognitive rehearsal of a task in the absence of overt physical movement” (Driskell, 79 , 481 - 492.). Imagining is a useful technique to achieve expertise. In problem solving, based on imagining techniques, students are asked to look at the steps that describe a procedure on how to solve a problem. Next, students are asked to close their eyes or look away from the material and deliberately try to visualize or verbalize the procedure. The imagination effect is dependent on the expertise level of the student. Reverse imagination effect occurs when students have a low expertise level because, in such a situation, studying information is more efficient than imagining it because students may find it difficult to imagine. In order to imagine information, a student must process the information in working memory, which would not be possible till schemas are formed in the long term memory. Until that time, studying content physically may be superior to imagining.
Experiment
The research study on imagination effect on Turing Machine was conducted using an experimental post test design.
Variables
Two variables were selected for this study. The details of an independent variable and dependent variables are shown in the Table 1
Table
Definition of Variables
Variable | Definition | Value |
Independent | Instructional Method | Problem solving using Conventional Method Problem solving using Imagination |
Dependent | Post-Test Score | Test Score |
The operational definition of teaching the method requires 4 one-hour classes for third year science students. An instructional method using imagination is the instructional strategy for the experimental group while the conventional method is the instructional strategy for the control group. Therefore, values of the independent variable for those who had the conventional method can be compared with those who used the imagination method. The post-test achievement score is the dependent variable. The value of the dependent variable is raw scores on the post-test.
Hypotheses
Using the Cognitive Load Theory and knowing high element interactivity in solving problems on Turing Machine, it was hypothesized that students learning the Turing Machine through the imagination method would outperform the students who would learn the machine through physical study of the material. As part of the hypothesis testing procedure, a null hypothesis was devised which stated that there would be no difference in performance of students learning from imagination and conventional study methods.
Participants
The sample selected for the experiment consisted of 30 students from third year computer science department of KTHM College, Nashik. The students were randomly distributed into the two groups, each consisting of 15 students.
Experimental design
The two-group posttest-only randomized experiment, despite its simple structure, was selected for the study as it is one of the best research designs for assessing cause-effect relationships. One group was the control group which received instruction using the conventional method. The second group was the experimental group which received instruction using the imagination method. Because the participants were randomly distributed into the two groups, a pre-test was not conducted to verify the equivalence of two groups.
Material and Instruments
A questionnaire was prepared on topics in the “Theory of Computing” syllabus for a third year science program. A five-point rating scale was used in the questionnaire to judge the level of difficulty of various topics in the syllabus. Difficult topics were identified. Turing Machine, Finite Automata and Push Down Automata were found to be some of the difficult topics. The instructional material on the Turing Machine was prepared in the form of a PowerPoint presentation, animation, graphics, solved problems and imagination problems. An achievement test was devised to test the performance of students in solving problems based on the Turing Machine.
Treatment
A lesson plan consisting of four lectures on Turing Machine was prepared. Each lecture consisted of 20 minutes of face-to-face instruction, 10 minutes for student interaction and 20 minutes for problem solving.
Lectures were delivered on 4 different days using Power Point slides containing graphics and animations. Students of both the groups attended the lecture of the same teacher. Then the students were divided into control and experimental group for solving problems on the Turing Machine.
The students were given pairs of problems. Each pair consisted of a worked example and a problem to be solved. Instructions were given to the control group students to study the worked problems without using imagination. Students in the experimental group were asked to study the worked problems using imagination. Then both groups were asked to solve a problem which was very similar to the worked problem that students had already studied.
Results and Discussions
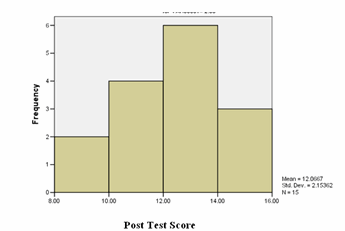
The number of correct answers was the test score. The t-test was used for testing the hypotheses. As a pre-requisite for t-test, the score was analyzed to verify normality. The observation of histograms given in Figure 1 shows the normality of score distributions.
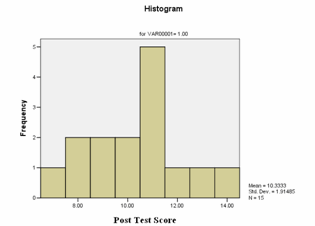
Figure 1. Histogram for score distribution of control group
Figure 2. Histogram for score distribution of experimental group.
Table 2
Tests of Normality

The test score of the two groups of students was found to be normal.
The results given in Table 2 show that Kolmogorov-Smirnov (control: p=0.200, experimental: p=0.200) and Shapiro-Wilk test (control: p=0.757, experimental: p=0.951) for normality are not significant and hence distributions of scores are normal. The means and standard deviations are given in the Table 3.
Group Statistics
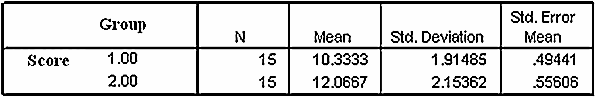
The summary of t-test results is given in Table 4.
Table 4
Independent Samples Test
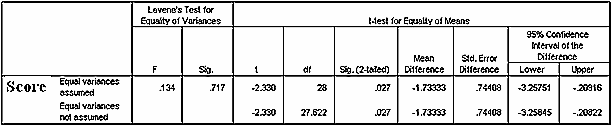
The t-test is significant (p=.027 <.05) at the assumed level of significance of .05. Hence, the null hypothesis is rejected and the alternative hypothesis is supported. The alternate hypothesis states that students learning through imagining method outperform students learning though study method.
Conclusion
The experiment covered in this paper examined the imagination effect on learning the Turing Machine. The results provided evidence for the hypothesized improvement in learning from the method which used mental imagination than the learning done through study of material. The cognitive load theory predicts that imagination effect is prominent when students are learning high interactivity material. In case of low interactivity material, the imagination effect is not negligible because overall cognitive load is small and can easily be processed the working memory. On contrary, cognitive load of the content on Turing Machine is high because it involves many elements of information that need to be studied simultaneously.
After conducting lectures on the Turing Machine and solving problems in the classroom, students are able to construct a sufficient number of schemas to understand the steps involved in given problems. By engaging students in imagining the procedure of solving problems, construction of higher level schemas, schema automation is achieved which helps students to perform better than those students who simply study the Turing Machine without imagining procedures. Studying the Turing Machine is a redundant activity which interferes with learning process.
Similar experiments were conducted for topics on Finite Automata and Pushdown Automata. The results of these experiments also show that the learning is enhanced when students are engaged, after delivering lectures and solving problems, and in imagining procedures required for solution of additional problems. It is found that students are reluctant to study the material and carry out problem solving steps on paper because the number of state transitions, stack operations and head movements are large in number which requires considerable time and effort to solve problems. Hence, engaging students in imagining procedures is a good alternative for the teaching as well as the learning process.
Bibliography
Baddeley, A. (1994). The magical number seven: still magical after all these years? Psychological Review , 101(2), 353-356.
Chandler P., S. J. (1991). Cognitive load theory and the format of instruction. Cognition and Instruction , 293-332.
Chi, M. T. (1982). Expertise in problem solving. In R.J. Sternberg(Ed.). Advances in the Psychology of Human Intelligence , Vol.1, 7-75.
Clark Ruth Colvin, N. F. (12 October 2006). Performance Improvement. International Society forPerformance Improvment , Volume 45 Issue, 46-47.
Cooper, G. (1998). Research into Cognitive Load Theory and Instructional Design at UNSW. Australia: University of New South Wales.
Driskell, J. E. (79 , 481 - 492.). Does mental practice enhance performance? . Journal of Applied Psychology , 79 , 481 - 492.
Hodges, A. (Mrch, 1992). Alan Turing: The Enigma (Paperback). London: Vintage, Random House.
Kleene, S. (1952). Introduction to Mathematics. amsterdam netherlands: North-Holland Publishing Company.
Larkin, J. H. (1980). Models of competence in solving physics problems. Cognitive Science , Vol. 4, Issue 4, 317-345.
Mealy, G. H. (1955). A method for synthesizing sequential circuits. Bell Systems technical Journal , 34, 1045-1079.
Miller, G. A. (1956). The magical number seven, plus or minus two: Some limits on our capcity for processing information. Psychol. Rev., 63, 81-97.
Pass F., R. A. (2004). Cognitive Load theory: Instructional Implications of Interaction betwen Information Structures and Cognitive Architecture. Instructional Science , 1-8.
Pass, F. R. (2003). Cognitive load theory and instructional design: Recent developments . Educational Psychologist , 31, 1-15.
Post, E. (1943). Reductions of the general Combinatorial Decision Problem. American Journal of Mathematics , 65, 197-215.
Rowland, T. (2009). From MathWorld--A Wolfram Web Resource, created by Eric W. Weisstein. Retrieved February 2009, from WolframMathWorld: http://mathworld.wolfram.com/Church-TuringThesis.html
Sakharov, A. ". (2009). MathWorld-A Wolfram Web Resource, created by Eric W. Weisstein. Retrieved February 2009, from http://mathworld.wolfram.com/KleenesRecursionTheorem.html
Schneider, W. a. (1977). Controlled and automatic human information processing: I. Detection, search and attention. Psychology Review , 84: 1-66.
Shiffrin, R. &. (1977). Controlled and automatic human information processing: II. Perceptual learning, automatic attending, and a general theory. Psychology Review , 84: 127-190.
Shiffrin, R. M. (1994). Seven plus or minus two: a commentary capacity limitations. Psychological Review , 101(2), 357-361.
Shiffrin, R. M., & Atkinson, R. C. (1969). Storage and retrieval processes in long-term memory. Psychological Review , 179-193.
Stoltzfus, E. R. (1996). Working memory and aging: current status of the inhibitory view. In T. E. Richardson, R. W. Engle, L. Hasher, R. H. Logie, E. R. Stoltzfus, & R. T. Zacks (Eds.), Working memory and human cognition. New York: Oxford University Press.
Sweller John, J. J. (1998). Cognitive Architecture and Instructional Design. Educational Psychology , Vo. 10, No.3.
Sweller, J. (1988). Cognitive load during problem solving, Effects on learning. Cognitive Science, 12, 257-285.
About the Authors
| Ramchandra Satyadeo Tiwari is Director, School of Computer Science, Yashwantrao Cahavan Maharashtra Open University, Nashik-5. He is MSc in Physics currently completing a Ph.D. He has 34 years of experience in the computer field including 17 years development of Computer Programmes for the Open Education System and major work in satellite image processing for remote sensing and multimedia, computer graphics for education. As visiting faculty he taught Software Engineering at the KKW College of Engineering and Windows Programming at RYK Science College Nashik. He is winner of the “Yashokirti Award” by the Computer Society of India He is a Former Member of the Board of Studies, Computer Science University of Pune, Chairman of the School Council for Computer Science, YCM Open University, Member of the Academic Council, YCM Open University, and Former Member of the Board of Studies, Computer School, Indira Gandhi National Open University), New Delhi. R S Tiwari |
| Sunita Nimba Deore, M.C.M., M.C.S. is Lecturer in the Computer Science Department, K.T.H.M.College, Nashik-2. She has 15 years of experience of teaching computer courses to undergraduate and postgraduate students, was exam maker and examiner at University of Pune, and visiting faculty at Indira Gandhi National Open University (IGNOU). She has a special interest in Theoretical Computer Science, Object Oriented Software Engineering, and Modeling languages like UML She is advisor and guide to graduate and postgraduate level students S N Deore |